गुरुत्वाकर्षण

गुरुत्वाकर्षण बल

ब्रह्मांड में सभी वस्तुएँ एक-दूसरे को आकर्षित करती हैं। इस आकर्षण बल को गुरुत्वाकर्षण बल कहते हैं।

न्यूटन के प्रेक्षण

सेब पेड़ से नीचे धरती की ओर क्यों गिरता है?
क्योंकि पृथ्वी उसे अपनी ओर आकर्षित करती है।

अभिकेंद्रीय बल

जब कोई पिंड वृत्ताकार पथ पर गति करता है, तो वह प्रत्येक बिंदु पर अपनी दिशा बदलता है। वह बल जो पिंड को वृत्ताकार पथ पर गति कराता है, वृत्त के केंद्र की ओर कार्य करता है। इस बल को अभिकेंद्रीय बल कहते हैं।

महत्वपूर्ण बिंदु

यदि अभिकेंद्रीय बल न हो, तो पिंड वृत्ताकार पथ के स्पर्श रेखा के अनुदिश सरल रेखा में गति करेगा।

गुरुत्वाकर्षण का सार्वत्रिक नियम

न्यूटन का गुरुत्वाकर्षण नियम (1687)-

गुरुत्वाकर्षण का सार्वत्रिक नियम कहता है कि, 'ब्रह्मांड का प्रत्येक पिंड अन्य प्रत्येक पिंड को एक बल से आकर्षित करता है, जो उनके द्रव्यमानों के गुणनफल के अनुक्रमानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।'

गणितीय निरूपण

माना दो पिंडों के द्रव्यमान \( m_1 \) और \( m_2 \) हैं तथा उनके बीच की दूरी \( d \) है, तो उनके बीच आकर्षण बल:

\[ F \propto m_1 \times m_2 \quad \text{(i)} \] \[ F \propto \frac{1}{d^2} \quad \text{(ii)} \]

उपरोक्त समीकरणों से हम लिख सकते हैं:

\[ F \propto \frac{m_1 m_2}{d^2} \] \[ F = \frac{G m_1 m_2}{d^2} \]

जहाँ \( G \) गुरुत्वाकर्षण नियतांक है।

SI मात्रक: \( Nm^2 kg^{-2} \)
\( G \) का मान: \( 6.673 \times 10^{-11} Nm^2 kg^{-2} \) (हेनरी कैवेंडिश द्वारा निर्धारित)

गुरुत्वाकर्षण के सार्वत्रिक नियम का महत्व

हमें पृथ्वी से बांधे रखता है
चंद्रमा की पृथ्वी के चारों ओर गति को नियंत्रित करता है
पृथ्वी की सूर्य के चारों ओर गति की व्याख्या करता है
चंद्रमा के कारण समुद्र में ज्वार-भाटा उत्पन्न करता है

मुक्त पतन

मुक्त पतन: जब कोई वस्तु केवल पृथ्वी के गुरुत्वाकर्षण बल के अंतर्गत नीचे गिरती है, तो इसे मुक्त पतन कहते हैं।

गुरुत्वीय त्वरण: मुक्त पतन के दौरान पृथ्वी के गुरुत्वाकर्षण के कारण वस्तु द्वारा प्राप्त त्वरण को गुरुत्वीय त्वरण कहते हैं।

इसे 'g' से निरूपित करते हैं
SI मात्रक = \( ms^{-2} \) (त्वरण के समान)

पृथ्वी की सतह पर 'g' का मान

हम जानते हैं कि वस्तु पर कार्यरत बल:

\[ F = \frac{G M_e m}{R^2} \quad \text{(i)} \]

जहाँ:
\( M_e \) = पृथ्वी का द्रव्यमान
\( m \) = वस्तु का द्रव्यमान
\( R \) = पृथ्वी की त्रिज्या

हम गति के द्वितीय नियम से जानते हैं:

\[ F = mg \quad \text{(ii)} \]

समीकरण (i) और (ii) से, हम पाते हैं:

\[ m \times g = \frac{G M_e m}{R^2} \] \[ g = \frac{G M_e}{R^2} \]

जब कोई पिंड पृथ्वी के केंद्र से 'r' दूरी पर हो तो:

\[ g = \frac{G M}{r^2} \]

महत्वपूर्ण बिंदु

'g' का मान पृथ्वी के विभिन्न स्थानों पर भिन्न हो सकता है:

समीकरण \( g = \frac{G M}{r^2} \) से स्पष्ट है कि g का मान \( r \) (पृथ्वी के केंद्र से वस्तु की दूरी) पर निर्भर करता है।
क्योंकि पृथ्वी का आकार पूर्ण गोला नहीं है - यह ध्रुवों पर चपटी और विषुवत वृत्त पर उभरी हुई है।
अतः 'g' का मान ध्रुवों पर अधिक और विषुवत वृत्त पर कम होता है। परंतु सुविधा के लिए हम 'g' को नियत मान लेते हैं।

g की गणना \[ g = \frac{G M}{R^2} \] \[ = \frac{6.673 \times 10^{-11} \times 6 \times 10^{24} kg}{(6.4 \times 10^6 m)^2} \] \[ g = 9.8 ms^{-2} \]

पृथ्वी का द्रव्यमान = \( 6 \times 10^{24} kg \)

पृथ्वी की त्रिज्या = \( 6.4 \times 10^6 m \)

मानक मान: \( g = 9.8 ms^{-2} \)

G और g में अंतर

गुरुत्वाकर्षण नियतांक (G)	गुरुत्वीय त्वरण (g)
1. इसका मान \( 6.673 \times 10^{-11} Nm^2/kg^2 \) होता है।	1. इसका मान \( 9.8 m/s^2 \) होता है।
2. इसका मान सर्वत्र समान रहता है।	2. इसका मान अलग-अलग स्थानों पर भिन्न होता है।
3. इसका मात्रक \( Nm^2/kg^2 \) है।	3. इसका मात्रक \( m/s^2 \) है।
4. यह एक अदिश राशि है।	4. यह एक सदिश राशि है।

मुक्त पतन के लिए गति के समीकरण

                    स्थिति 1: प्रारंभिक वेग (u) से पृथ्वी की ओर गिरती हुई वस्तु
                    \[ v = u + gt \]
                    \[ s = ut + \frac{1}{2}gt^2 \]
                    \[ v^2 = u^2 + 2gh \]
                

                    स्थिति 2: विरामावस्था से गिरती हुई वस्तु (प्रारंभिक वेग u=0)
                    \[ v = gt \]
                    \[ s = \frac{1}{2}gt^2 \]
                    \[ v^2 = 2gh \]
                

स्थिति 3: प्रारंभिक वेग (u) से ऊपर की ओर फेंकी गई वस्तु

गुरुत्वीय त्वरण (g) ऋणात्मक होगा:

\[ v = u - gt \] \[ s = ut - \frac{1}{2}gt^2 \] \[ v^2 = u^2 - 2gh \]

द्रव्यमान और भार

द्रव्यमान

किसी वस्तु का द्रव्यमान उसकी जड़ता का माप है।

SI मात्रक = किलोग्राम (kg)
द्रव्यमान एक अदिश राशि है।
वस्तु का द्रव्यमान नियत रहता है।
वस्तु का द्रव्यमान शून्य नहीं हो सकता।

भार

वह बल जिससे कोई वस्तु पृथ्वी के केंद्र की ओर आकर्षित होती है, उस वस्तु का भार कहलाता है।

हम जानते हैं, बल = द्रव्यमान × त्वरण:

\[ F = m \times g \quad (\text{क्योंकि } a = g) \]

उपरोक्त परिभाषा से, यह बल भार है अतः:

\[ W = m \times g \]

SI मात्रक = न्यूटन (N)
सदिश राशि।

चंद्रमा पर वस्तु का भार

चंद्रमा का द्रव्यमान पृथ्वी से कम होने के कारण यह वस्तुओं को कम बल से आकर्षित करता है।

महत्वपूर्ण निष्कर्ष

चंद्रमा पर किसी वस्तु का भार पृथ्वी पर उसके भार का 1/6 भाग होता है।

प्रणोद और दाब

क) प्रणोद

प्रणोद वह बल है जो किसी वस्तु पर सतह के लंबवत कार्य करता है।

उदाहरण

जब आप ढीली रेत पर खड़े होते हैं तो आपके शरीर का बल (भार) आपके पैरों के क्षेत्रफल के बराबर क्षेत्र पर कार्य करता है। जब आप लेट जाते हैं, तो यही बल पूरे शरीर के संपर्क क्षेत्र पर कार्य करता है। दोनों स्थितियों में रेत पर कार्यरत बल (प्रणोद) समान होता है।

ख) दाब

दाब प्रति इकाई क्षेत्रफल पर कार्य करने वाला बल है।

\[ \text{दाब} = \frac{\text{प्रणोद}}{\text{क्षेत्रफल}} \]

उदाहरण

ढीली रेत पर प्रणोद का प्रभाव खड़े होने की तुलना में लेटने पर कम होता है।

प्रणोद का SI मात्रक \( N/m^2 \) या \( N m^{-2} \) है।
इसे पास्कल (Pa) भी कहते हैं।

तरलों में दाब

क) तरलों (द्रव और गैस) में दाब

तरल पात्र की तली और दीवारों पर दाब डालते हैं
तरल सभी दिशाओं में दाब डालते हैं
तरलों पर डाला गया दाब सभी दिशाओं में समान रूप से संचरित होता है

ख) उत्प्लावन बल (उत्क्षेप)

जब कोई वस्तु किसी तरल में डुबोई जाती है तो उस पर एक ऊपर की दिशा में बल कार्य करता है जिसे उत्प्लावन बल कहते हैं। इस गुण को उत्प्लावन या उत्क्षेप कहते हैं।

गुरुत्वाकर्षण बल वस्तु को नीचे की ओर खींचता है और उत्प्लावन बल उसे ऊपर की ओर धकेलता है।

उत्प्लावन बल का परिमाण तरल के घनत्व पर निर्भर करता है।

ग) वस्तुएँ पानी में क्यों तैरती या डूबती हैं?

यदि किसी वस्तु का घनत्व तरल के घनत्व से कम होता है, तो वह तरल पर तैरती है और यदि वस्तु का घनत्व तरल के घनत्व से अधिक होता है, तो वह तरल में डूब जाती है।

गतिविधि

एक बीकर में कुछ पानी लें। समान द्रव्यमान का कॉर्क का टुकड़ा और लोहे की कील लें। उन्हें पानी पर रखें। कॉर्क तैरता है और कील डूब जाती है।

कॉर्क इसलिए तैरता है क्योंकि कॉर्क का घनत्व पानी के घनत्व से कम होता है और पानी का उत्प्लावन बल कॉर्क के भार से अधिक होता है।
कील इसलिए डूबती है क्योंकि लोहे की कील का घनत्व पानी के घनत्व से अधिक होता है और पानी का उत्प्लावन बल कील के भार से कम होता है।

आर्किमिडीज का सिद्धांत

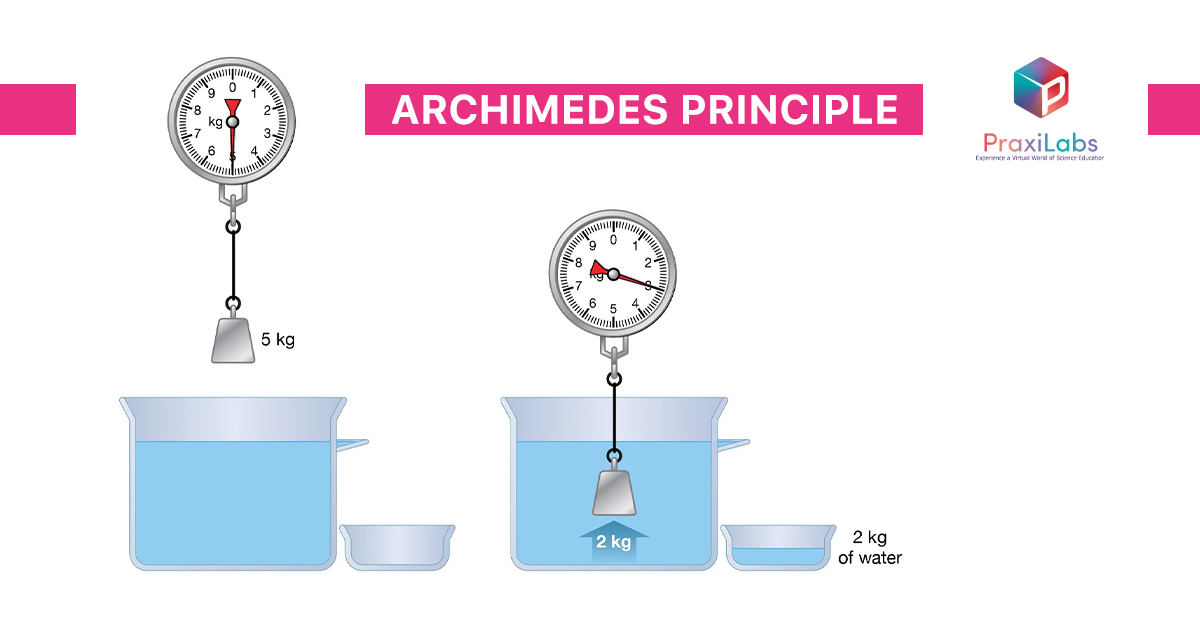
आर्किमिडीज का सिद्धांत कहता है कि, 'जब कोई वस्तु किसी तरल में आंशिक या पूर्ण रूप से डुबोई जाती है, तो उस पर एक ऊपर की दिशा में बल कार्य करता है जो उस वस्तु द्वारा विस्थापित तरल के भार के बराबर होता है।'

अनुप्रयोग

आर्किमिडीज के सिद्धांत के अनेक उपयोग हैं:

इसका उपयोग जहाजों और पनडुब्बियों के डिजाइन में किया जाता है
द्रवों का घनत्व मापने वाले हाइड्रोमीटर में
दूध की शुद्धता जांचने वाले लैक्टोमीटर में

घनत्व और आपेक्षिक घनत्व

i) घनत्व

किसी पदार्थ का घनत्व उसके एकांक आयतन का द्रव्यमान होता है।

\[ \text{घनत्व} = \frac{\text{द्रव्यमान}}{\text{आयतन}} \]

घनत्व का मात्रक किलोग्राम प्रति घन मीटर \( (kg m^{-3}) \) है।

ii) आपेक्षिक घनत्व

किसी पदार्थ का आपेक्षिक घनत्व उस पदार्थ के घनत्व और जल के घनत्व का अनुपात होता है।

\[ \text{आपेक्षिक घनत्व} = \frac{\text{पदार्थ का घनत्व}}{\text{जल का घनत्व}} \]

महत्वपूर्ण बिंदु

चूँकि आपेक्षिक घनत्व समान राशियों का अनुपात है, इसका कोई मात्रक नहीं होता।